Math, Visual Play, and the Creative Process
I am not a mathematician. I am a graphic designer. Like most people, though, I did have some kind of relationship with math in my former years – a bad one. I was subjected to three years of college-level math in high school, and I resented it. I didn’t hate it, exactly, but the majority of the curriculum seemed to be dedicated to answering contrived questions using prescribed formulas. The initial explanation of a new concept was often interesting, but this quickly devolved into an instructional on the rote mechanics of plugging numbers into the appropriate equations. It wasn’t useful, and it certainly wasn’t fun.
Ideas in math are abstract; they deal with imaginary objects. Even the basic concept of numbers is an abstraction. Sure, we can use concrete examples to describe a specific number, but how do we define the commonality between five dogs, five days, and five inches? This in itself can be a hurdle, especially for more visual-spatial thinkers. But then we add another hurdle. We use abstract symbols to represent these abstract ideas: we use numerals to represent numbers, letters to represent variables and constants, and strange symbols to represent operations and functions.
1 2 3
x y a b c
+ − × ÷ =
Symbolic notation is a useful tool. Our understanding of math might be largely due to our ability as a species to use symbolic representation Dehaene 2011, chap. 4. But manipulating these symbols seems pretty meaningless if you don’t already have a clear understanding of what the symbols represent. I could never memorize mathematical formulas. If I needed to use a formula, I would have to break it down until it made sense to me. Then I could reconstruct it as needed. If I couldn’t figure it out on my own, I’d ask my teacher to break it down for me (I was a “difficult” student in that way).
When the majority of students did not understand a concept well, the teachers would roll out the mnemonics, like “SohCahToa” (sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, tangent = opposite/adjacent). Why did we depend on sound associations to memorize formulas? Why didn’t we spend more time exploring the fundamentals so we could grasp the meaning of the formulas? The last thing we needed was another level of abstraction to obscure matters further. No wonder I gave up math for art.
Compare abstract mathematical concepts to what we describe as “abstract” in the visual arts. Abstract art is non-representational. In other words, it does not represent something else that is already recognizable in our world, like a person, object, or place. Yet it physically exists as something we can directly experience in our perceptual world and not merely in our heads. The meaning of the work is embedded in the direct experience of it. I preferred this type of abstraction. Compared to art, math seemed trite and would likely lead to a life of boring accounting work (both my parents were trained as accountants – that might have had something to do with this theory of mine). No, I was creative, and therefore could never be a mathematician. The beginning of college was pretty much the end of my math education.
A decade later, I’ve come to realize that math is a creative process. Not all aspects of math are creative – not the tedious calculations, which involve memorizing the multiplication table (I still get it wrong) and plugging numbers into formulas. But some aspects are creative, like when you get to discover strange, intriguing, beautiful patterns and attempt to understand their existence:

Fig 1 Why does the sum of all consecutive odd numbers always equal a square number? Strogatz 2012
If you’re skeptical about the artistic value of math, read Paul Lockhart’s essay, "A Mathematician’s Lament" 2002, the most convincing argument I’ve read on the topic. Lockhart laments the state of math education, with its over-emphasis on rote memorization and calculation and under-emphasis on actual mathematics:
By concentrating on what, and leaving out why, mathematics is reduced to an empty shell. The art is not in the "truth" but in the explanation, the argument. It is the argument itself which gives the truth its context, and determines what is really being said and meant. Mathematics is the art of explanation.
Paul Lockhart
How can we experience math as a creative process? What kinds of activities encourage creative thinking? I don’t have much experience with math, but I have spent most of my life actively involved in creative processes. I wondered what I could translate from my personal experience in visual arts and graphic design to math. The aspects that I identified all had the same unifying factor: they were all qualities of play. Many people more qualified than myself have studied the link between creativity and play, including art educator Carol Becker 2009, play researcher Stuart Brown, and graphic designer Paul Rand 2012. Artists and designers know how to play.
However, playing with abstract ideas is tricky. We can’t poke them, turn them inside out, or change their color. We can only think about them. Playing with symbols that represent abstract ideas is tricky, too, if we don’t already have a clear understanding of the abstract ideas they represent. Some research shows that our understanding of number is primarily contained in the visual-spatial region of our brains Dehaene 2011, so perhaps we can play through visual-spatial means. As a graphic designer, I prefer to play with visuals – that is, I like to observe, question, and manipulate objects in the world in order to affect the way they look.
I’ve been drawing for fun my whole life, but my first drawing class in college changed the way I understood this activity. Drawing, my professor said, is the process of looking closely at something in order to understand it. To make a visible mark is to attempt to make a statement about the nature of your subject (whether it exists in your physical world or in your imagination). Drawing also creates evidence of physical paths through space. It reveals patterns of movement through visual patterns. One of my favorite childhood toys, the Spirograph, is a great example of this: you use it to draw intricate curves that reveal the complex path created by a seemingly simple system of one circle rotating inside another. In a broad sense, the act of drawing is any act of creating an image through making marks or manipulating material. I think that this is an essential part of what it means to play in a visual way.

Using the framework of math exploration through visual play, I developed a collection of ongoing projects that I call Play Math. These projects exemplify the qualities of visual play that are important in my own creative processes as a graphic designer.
To play is to freely pursue many different questions, within constraints. Color by Numbers is a play set about number patterns and sequences that allows players to choose different levels of freedom, from answering specific questions about given number patterns to inventing ways of combining patterns to creating their own patterns. In education, these prompts and restrictions have been called liberating constraints Davis, Sumara and Luce-Kapler 2000 and they allow you to generate lines of inquiry that are most personally interesting without being paralyzed by infinite possibilities. Play is not about following one single path established by someone else (that would be boring), but about starting at an established point and discovering your own paths.
To play is to consider that there may be no single right answer, but rather many answers to every problem. One, Two, or Three? is a game where all possible answers – one, two, and three – are correct Fig 2. The challenge, then, is not to come up with the right answer, but to reflect on why you make the choices you do, and how these choices can change in different circumstances.

Fig 2 One, Two, or Three? What number comes to mind when you see this image?
One of my favorite books as a child was a little black and white book of optical illusions, featuring Rubin’s vase on the cover (the famous image of a white vase and two black faces, demonstrating reversing figure-ground relationships). I was always fascinated with graphic optical illusions and magic-eye posters, but I was even more fascinated with real-life illusions. As a child, I traveled a lot by plane. I would play the same game every time I was at the baggage carousel waiting for my luggage: I would focus my eyes intently on the moving carousel – as if it were a magic eye poster – until I tricked my brain into thinking that the carousel was still and it was myself (and the rest of the airport) that was spinning around the carousel. To me it was magic – to actively change not only the way you see the world, but the way you experience being in the world.

To play is to constantly shift perspectives – that is, to perceive and interpret the same external stimuli in different ways by focusing on different aspects. Vertex by Vertex is an exploration of geometric tiling that uses vertices (points where lines meet) as the constituent building blocks, rather than the geometric shapes themselves. Constructing non-repeating patterns one vertex at a time is one possible strategy for exploring the systematic nature of geometric tiling. I call this project Vertex by Vertex to highlight the method of determining each new addition, but engaging in this process actually involves constantly shifting focus between vertices and shapes. Creating certain physical manifestations of this system (such as sculptures made out of drinking straws) also requires shifting focus to the single line itself as the unit.
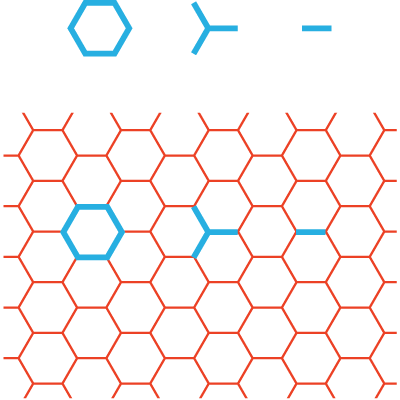
Fig 3 Regular hexagonal tiling and its various building blocks.
In middle school, I had a math textbook with M.C. Escher’s famous lithography, Ascending and Descending, on the cover. I was fascinated by this depiction of the Penrose stairs, an impossible staircase that perpetually travels up (or down). We made paper models to witness firsthand this impossible object. From most perspectives the physical gap in the spiraling staircase was visible, but at just the right perspective, the two ends of the staircase appeared to connect, creating the infinitely looping staircase.

To play is to let go of literal and physical “truths” in representation – to take poetic liberties in order to create authentic yet novel experiences. Poetic Algorithm of One expresses a pattern in arithmetic that is normally not easily accessible because of the vast shift in magnitude of the numbers. Through a visual compression of the space between the numbers, the pattern emerges as something we can visually perceive. It is not a physically true representation in a logical sense, but it is a more illuminating translation of a mathematical pattern to something we can directly perceive, and actually closer to the way we mentally represent the magnitude of numbers Dehaene 2011. We can perhaps find more poignant expressions of mathematical patterns if we are less literal and more imaginative.
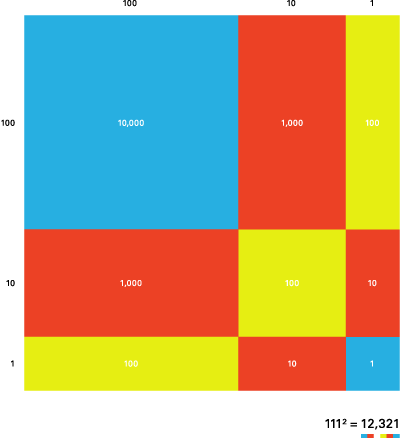
Fig 4 Poetic Algorithm of One, 111 ²
My impetus for Play Math was a desire to create visual tools and activities for others to engage with math, but more and more throughout the process, I’ve seen that it is just as much a project about my own personal engagement with math in creating these tools and activities. A theme that runs throughout Play Math is the idea that each project is not one single designed object or experience. I’ve developed each through multiple manifestations and media, which allowed me to be more playful: to explore many questions and many answers, to shift perspectives, and to be less literal. I don’t claim that this collection of projects is a comprehensive or balanced exploration of the scope of mathematical concepts. It is my personal journey of open-ended inquiry and problem-solving, based on where my own curiosity took me.
I’ve had a lot of fun, and I wish for everyone the opportunity to play with math in a personally meaningful way. Why can’t we all be mathematicians? We can all be artists: we can doodle on napkins, snap photos of our dogs, or make snow angels on the ground. We can all be musicians: we can strum guitars, sing along to the radio, or clap our hands to the beat. We can all be athletes: we can shoot hoops, throw frisbees, or ride bikes. Some of us may be more graceful than others in these endeavors, but who cares? To play is to focus on the experience itself, not the outcome. We’re free to explore as many possibilities as we can imagine because it doesn’t matter where we end up. That’s the beauty of play.
Problems lead you to where they take you. Art is not a race.
Paul Lockhart